Tijdens de rekenles vond ik optellen altijd interessanter dan aftrekken. Die voorkeur veranderde al snel tijdens mijn vroege puberjaren, maar het hele idee van optellen blijft iets bijzonders. Het is simpel maar erg krachtig, want je kunt ieder denkbaar getal vergroten. Probeer het maar eens uit. 1 + 1 = 2. 100 + 5 = 105. Het getal van Graham eindigt nadat je er 1 bij optelt ineens op een 8.

Maar wat als je oneindig lang doorgaat? Heeft de eindeloze optelling 1 + 2 + 3 + 4 + 5 + … een uitkomst? Een wiskundig gehandicapte zoals ik denkt meteen van niet. Het is een oneindige reeks, en oneindig + 1 is nog altijd oneindig. Basta. Het jonge wiskundige genie Srinivasa Ramanujan dacht daar anders over. Hij beredeneerde dat deze optelling wel degelijk een uitkomst heeft. En wel -1/12. Yeah right.

In zijn brief aan de Britse geneticus G.H Hardy schreef Ramanujan ‘je zult me na het trekken van deze conclusie wel direct naar een gekkenhuis verwijzen’. Toch is zijn redenering vrij eenvoudig te volgen.

Neem de oneindige reeks A:

A = 1 – 1 + 1 – 1 + 1 – 1 + …

Ook hier is het niet meteen logisch dat er een concrete uitkomst volgt uit deze som. Maar we zijn er nog niet. Wanneer je A aftrekt van 1, krijg je de volgende vergelijking:

1 – A = 1 – (1 – 1 + 1 – 1 + 1 – …)

En wanneer je de haakjes hier wegwerkt (bedankt nog voor dit inzicht van het omwisselen van plus- en mintekens bij het weghalen van haakjes in VWO 4, meneer Jansen) krijg je:

1 – A = 1 – 1 + 1 – 1 + 1 – 1 + …

Als je goed kijkt, zie je dat dit dezelfde reeks is als A. Dus:

1 – A = A

Daaruit volgt dat 2 x A = 1, oftewel, A = ½.

Grappig, een oneindige reeks heeft in dit geval toch een uitkomst. We gaan door met een tweede gevalletje B:

B = 1 – 2 + 3 – 4 + 5 – 6 + …

Als we die reeks nu eens bij zichzelf optellen, krijgen we:

2 x B = (1 – 2 + 3 – 4 + 5 – 6 + …) + (1 – 2 + 3 – 4 + 5 – 6 + …)

Laten we ze eens onder elkaar zetten en de individuele cijfers bij elkaar optellen:

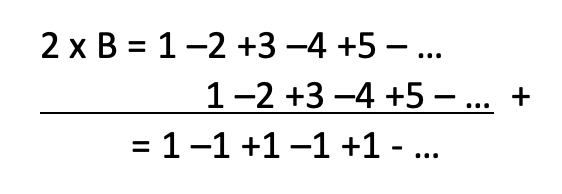
Dat resulteert in reeks A! Wie had dat gedacht:

2 x B = A = ½

B = ¼

Dan zijn we nu nog een enkele stap verwijderd van het eindresultaat. Laten we de oneindige optelling nog eens nemen:

S = 1 + 2 + 3 + 4 + 5 + …

En we trekken daar B vanaf:

S – B = (1 + 2 + 3 + 4 + 5 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …)

Dat gaat ook weer wat makkelijker als we ze onder elkaar zetten en de individuele cijfers van elkaar aftrekken:

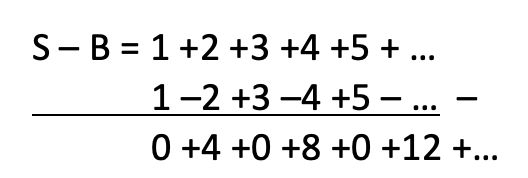
Oftewel S – B = 4 + 8 + 12 + …

En dat ziet er bekend uit, want dat is onze oneindige optelling vermenigvuldigd met vier:

S – B = 4 x S

We weten dat B = ¼, dus:

S – ¼ = 4 x S

Trekken we aan beide zijden een S af, houden we over:

– ¼ = 3 x S

Oftewel:

S = – 1/12

Verbluffend. De eindeloze optelling resulteert in een breuk net kleiner dan nul. En vergis je niet, dit is niet simpelweg een wiskundig trucje. De uitkomst van deze Ramanujan-som heeft directe toepassing gehad op modellen binnen de kwantumfysica van onder andere Hendrik Casimir.

Minstens zo belangrijk: deze hele berekening bewijst dat mijn pre-puberale fascinatie voor optellen legitiem was – heel veel optellen komt neer op een klein beetje aftrekken.